Euler-Lagrange Equation

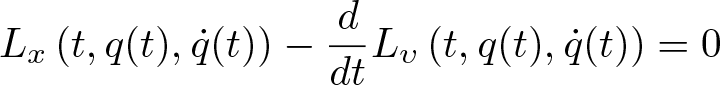
Discovered by: Leonhard Euler and Joseph-Louis Lagrange in the 1750s.

What is it? In the calculus of variations, the Euler-Lagrange equation is a second-order partial differential equation whose solutions are the functions for which a given functional is stationary.

Why is it important? Because a differentiable functional is stationary at its local maxima and minima, the Euler–Lagrange equation is useful for solving optimization problems in which, given some functional, one seeks the function minimizing or maximizing it. This is analogous to Fermat's theorem in calculus, stating that at any point where a differentiable function attains a local extremum its derivative is zero.